Ultimate Mind-blowing NCERT Class 10 Math 6.3 Solutions(प्रश्नावली 6.3).

प्रश्न 1: बताइए कि आकृति 6.34 में दिए त्रिभुजों के युग्मों में से कोण – कोण से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग अपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
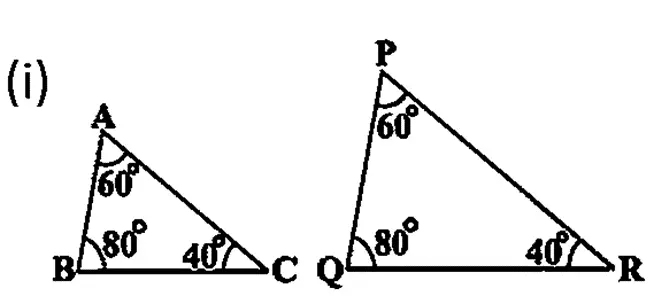
हल (i) :
ΔABC तथा ΔPQR में-
∠ABC = ∠PQR = 80°
∠BAC = ∠QPR = 60°
∠ACB = ∠PRQ = 40°
∴ AAA समरूपता कसौटी से-
ΔABC ~ ΔPQR
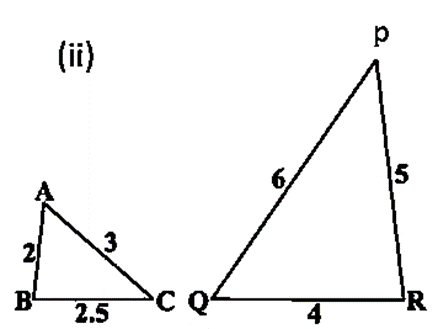
हल (ii) :
ΔABC तथा ΔQRP में-
AB/QR = BC/PR = AC/PQ = 1/2
∴ SSS समरूपता कसौटी से
ΔABC ~ ΔQRP
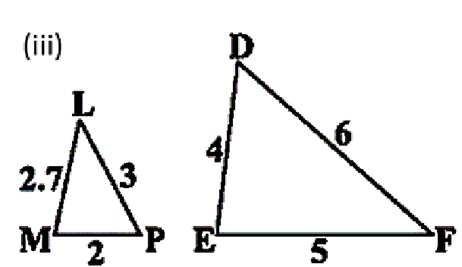
हल (iii) :
त्रिभुजो का यह युग्म समरूप नहीं है क्युकी सांगत भुजाये समानुपाती नहीं है |
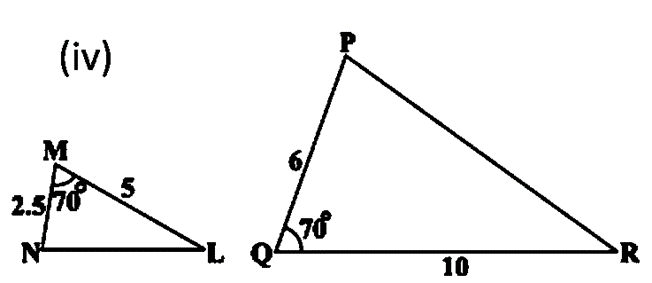
हल (iv) :
त्रिभुजो का यह युग्म समरूप नहीं है क्युकी सांगत भुजाये समानुपाती नहीं है |
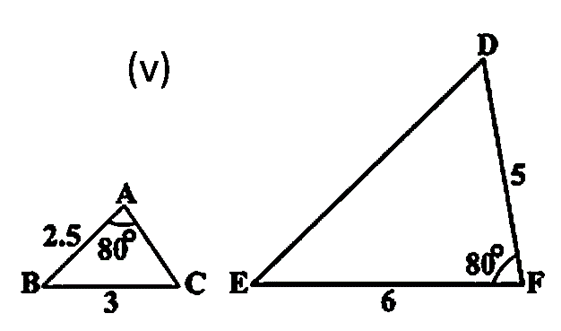
हल (v) :
त्रिभुजो का यह युग्म समरूप नहीं है क्युकी सांगत भुजाये समानुपाती नहीं है |
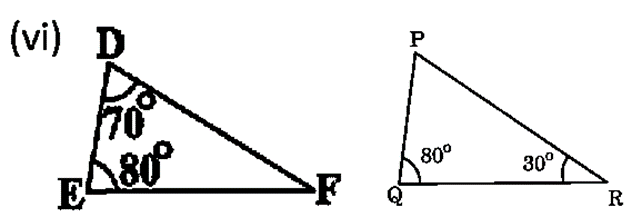
हल (vi) :
ΔDEF में,
∠D + ∠E + ∠F = 180°
⇒ 70° + 80° + ∠F = 180°
⇒ ∠F = 30°
इसीप्रकार, ΔPQR में,
∠P + ∠Q + ∠R = 180°
⇒ ∠P + 80° + 30° = 180°
⇒ ∠P = 70°
ΔDEF और ΔPQR में,
∠D = ∠P [प्रत्येक 70°]
∠E = ∠Q [प्रत्येक 80°]
∠F = ∠R [प्रत्येक 30°]
∴ ΔDEF ~ ΔPQR [AAA समरूपता कसौटी से]
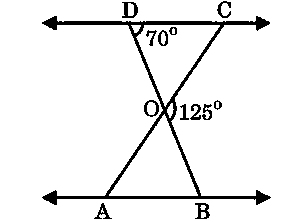
प्रश्न 2: आकृति में, ΔODC ~ ΔOBA, ∠BOC = 125° और ∠CDO = 70° है। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
हल 2:
DOB एक सरल रेखा है।
∴ ∠DOC + ∠COB = 180°
⇒ ∠DOC = 180° – 125° = 55°
∠DOC में,
∠DCO + ∠CDO + ∠DOC = 180°
⇒ ∠DCO + 70° + 55° = 180°
⇒ ∠DCO = 55°
दिया है, ΔODC ~ ΔOBA.
∴ ∠OAB = ∠OCD [समरूप त्रिभुजों के संगत कोण बराबर होते हैं]
∴ ∠OAB = 55°
प्रश्न 3 : समलंब ABCD, जिसमें AB // DC है, के विकर्ण AC और BD परस्पर O पर प्रतिछेद करते हैं। दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि OA/OC = OB/OD है।
हल 3:
दिया है : समलंब ABCD, जिसमें AB // DC है, के विकर्ण AC और BD परस्पर O पर प्रतिछेद करते हैं |
सिद्ध करना है : OA/OC = OB/OD
प्रमाण : AB // CD दिया है
∴ ∠ABO = ∠DCO (एकांतर कोण) …(1)
अब ΔAOB तथा ΔCOD में
∠ABO = ∠DCO (समीकरण (1) से)
∠AOB = ∠COD (शीर्षाभिमुख कोण)
A.A समरूपता कसौटी से
ΔAOB ~ ΔCOD
OA/OC = OB/OD (समरूप त्रिभुजों के संगत भुजा समानुपाती होते हैं|)
Proved

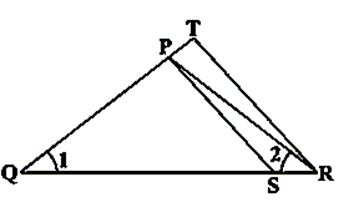
प्रश्न 4: आकृति में, QR/QS = QT/PR तथा ∠1 = ∠2 है। दर्शाइए कि ΔPQS ~ ΔTQR है।
हल 4 :
दिया है : QR/QS = QT/PR तथा ∠1 = ∠2 है |
सिद्ध करना है : ΔPQS ~ ΔTQR
प्रमाण : ΔPQR में,
∠1 = ∠2 (दिया है)
∴ PQ = PR (बराबर कोणों की सम्मुख भुजा) —(1)
और QR/QS = QT/PR (दिया है)
या, QR/QS = QT/PQ [समीकरण (1) से] ———- (2)
ΔPQS तथा ΔTQR में
QR/QS = QT/PQ [समीकरण (2) से]
∠1 = ∠1 (उभयनिष्ट)
SAS समरूपता कसौटी से
ΔPQS ~ ΔTQR
Proved
प्रश्न 5: ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दिखाईए कि ΔRPQ ~ ΔRTS है।
हल :
दिया है : DPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है |
सिद्ध करना है : ΔRPQ ~ ΔRTS
प्रमाण : ΔRPQ तथा ΔRTS में,
∠P = ∠RTS(दिया है )
∠R = ∠R (उभयनिष्ठ)
A.A समरूपता कसौटी से-
ΔRPQ ~ ΔRTS
PROVED.
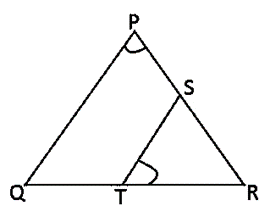
प्रश्न 6:
आकृति में, यदि ΔABE ≅ ΔACD हैं कि है, तो दर्शाइए कि ΔADE ~ ΔABC है।
हल:
दिया है : ΔABE ≅ ΔACD है
सिद्ध करना है : ΔADE ~ ΔABC
प्रमाण : ΔABE ≅ ΔACD (दिया है)
∴ AB = AC [सर्वांगसम त्रिभुजों की संगत भुजाएँ] ——–(1)
और, AD = AE [सर्वांगसम त्रिभुजों की संगत भुजाएँ] ———–(2)
ΔADE और ΔABC में,
AD/AB = AE/AC [समीकरण (1) और (2) से]
∠A = ∠A [उभयनिष्ठ]
∴ ΔADE ~ ΔABC [SAS समरूपता कसौटी से]
Proved.
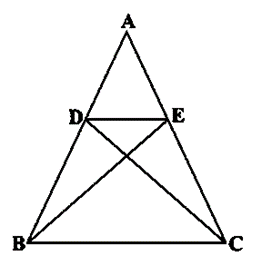
प्रश्न 7: आकृति 6.38 में, DABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिछेद करते हैं तो दर्शाइए कि :
(i) ΔAEP ~ ΔCDP
(ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB
(iv) ΔPDC ~ ΔBEC
हल 7:
दिया है : DABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिछेद करते हैं |
सिद्ध करना है :
(i) ΔAEP ~ ΔCDP
(ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB
(iv) ΔPDC ~ ΔBEC
प्रमाण:
(i)
ΔAEP और ΔCDP में,
∠APE = ∠CPD [शीर्षाभिमुख कोण]
∠AEP = ∠CDP [प्रत्येक 90°]
∴ ΔAEP ~ ΔCDP [AA समरूपता कसौटी से]
Proved.
(ii)
ΔABD और ΔCBE में,
∠ADB = ∠CEB [प्रत्येक 90°]
∠ABD = ∠CBE [उभयनिष्ठ]
∴ ΔABD ~ ΔCBE [AA समरूपता कसौटी से]
Proved.
(iii)
ΔAEP और ΔADB में,
∠AEP = ∠ADB [प्रत्येक 90°]
∠PAE = ∠DAB [उभयनिष्ठ]
∴ ΔAEP ~ ΔADB [AA समरूपता कसौटी से]
Proved.
(iv)
ΔPDC और ΔBEC में,
∠PDC = ∠BEC [प्रत्येक 90°]
∠PCD = ∠BCE [उभयनिष्ठ]
∴ ΔPDC ~ ΔBEC [AA समरूपता कसौटी से]
Proved.
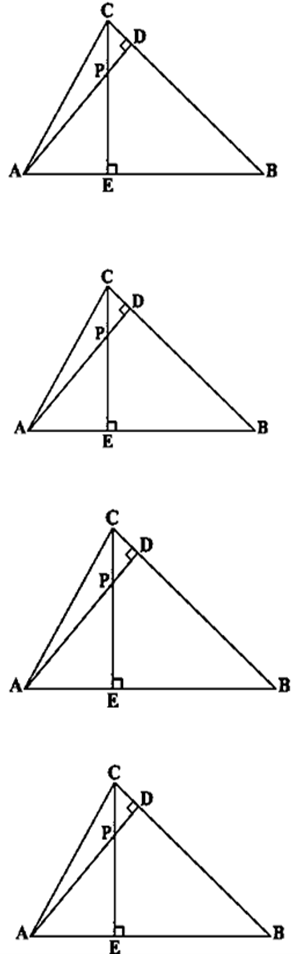
प्रश्न 8: समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा भुजा CD को पर प्रतिछेद करती है। दर्शाइए कि ΔABE ~ ΔCFB है।
हल 8:
दिया है : ABCD एक समांतर चतुर्भुज है जिसकी बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिछेद करती है।
सिद्ध करना है : ΔABE ~ ΔCFB
प्रमाण : ABCD एक समांतर चतुर्भुज है।
∠AEB = ∠CBE ———(1) [एकांतर कोण]
अब, ΔABE तथा ΔCFB में,
∠AEB = ∠CBE [समी0 (1) से ]
∠A = ∠C (समांतर चतुर्भुज के सम्मुख कोण)
ΔABE ~ ΔCFB [A.A समरूपता कसौटी से]
Proved.
प्रश्न 9: आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि:
(i) ΔABC ~ ΔAMP
(ii) AB/PQ = AD/PM
हल:
दिया है : ABC और AMP दो समकोण त्रिभुज हैं, जिसके कोण B और M समकोण हैं।
सिद्ध करना है :
(i) ΔABC ~ ΔAMP
(ii) AB/PQ = AD/PM
प्रमाण :
(i) ΔABC तथा ΔAMP में
∠ABC = ∠AMP (प्रत्येक 90°)
∠A = ∠A (उभयनिष्ठ)
∴ ΔABC ~ ΔAMP [A.A समरूपता कसौटी से]
Proved.
(ii) CA/PA = BC/MP
चूँकि समरूप त्रिभुज के सांगत भुजाये समानुपाती होती है|
Proved.
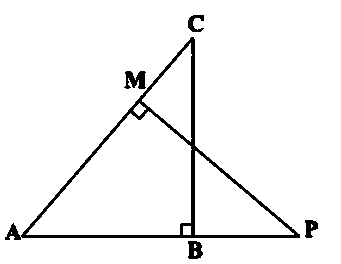
प्रश्न 10:
CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ΔABC और ΔFEG की भुजाओं AB और FE पर स्थित हैं। यदि ΔABC ~ ΔFEG है, तो दिखाइए कि:
(i) CD/GH = AC/FG
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
हल:
दिया है: CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ΔABC और ΔFEG की भुजाओं AB और FE पर स्थित हैं और ΔABC ~ ΔFEG है।
सिद्ध करना है : (i) CD/GH = AC/FG
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
प्रमाण : ΔABC और ΔFEG में-
ΔABC ~ ΔFEG (दिया है]
∠A = ∠F [समरूप त्रिभुज के संगत भुजा बराबर होता है|]
∠B = ∠E [समरूप त्रिभुज के संगत भुजा बराबर होता है|]
और, ∠C = ∠G [समरूप त्रिभुज के संगत भुजा बराबर होता है|]
∴ ∠ACD = ∠FGH [CD और GH समान कोणों के कोण समद्विभाजक हैं]
और, ∠DCB = ∠HGE [CD और GH समान कोणों के कोण समद्विभाजक हैं]
अब, ΔACD और ΔFGH में,
∠A = ∠F [ऊपर सिद्ध किया गया है]
∠ACD = ∠FGH [ऊपर सिद्ध किया गया है]
∴ ΔACD ~ ΔFGH [AA-समरूपता कसौटी से]
⇒ CD/GH = AC/FG
Proved.
(ii) ΔDCB और ΔHGE में,
∠DCB = ∠HGE [ऊपर सिद्ध किया गया है]
∠B = ∠E [ऊपर सिद्ध किया गया है]
∴ ΔDCB ~ ΔHGE [AA-समरूपता कसौटी से]
Proved.
(iii) ΔDCA और ΔHGF में,
∠ACD = ∠FGH [ऊपर सिद्ध किया गया है]
∠A = ∠F [ऊपर सिद्ध किया गया है]
∴ ΔDCA ~ ΔHGF [AA-समरूपता कसौटी से]
Proved.
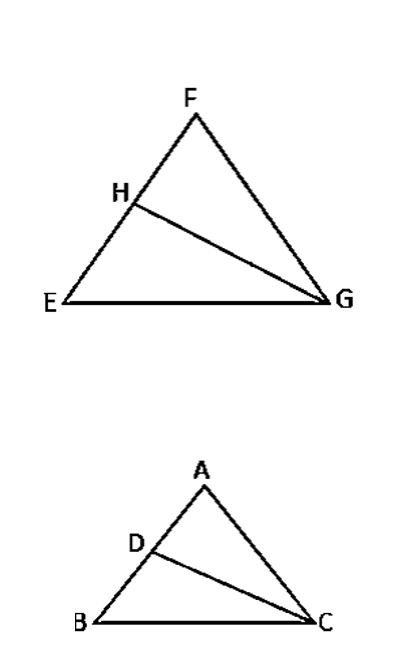
प्रश्न 11:
आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD⊥BC और EF⊥AC है तो सिद्ध कीजिए कि ΔABD ~ ΔECF है।
हल:
दिया है : AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिन्दु है जिसमें AD⊥BC और EF⊥AC है|
सिद्ध करना है : ΔABD ~ ΔECF
प्रमाण : ΔABC में,
AB = AC (दिया है)
∴ ∠B = ∠C ———(1) (बराबर भुजाओं के सम्मुख कोण)
अब, ΔABD तथा ΔECF में
∠ADB = ∠EFC (प्रत्येक 90°)
∠B = ∠C [समीकरण (1) से]
A.A समरूपता कसौटी से-
ΔABD ~ ΔECF
Proved.
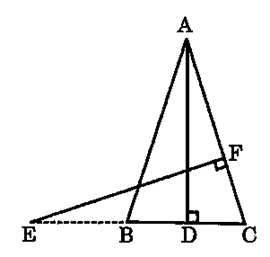
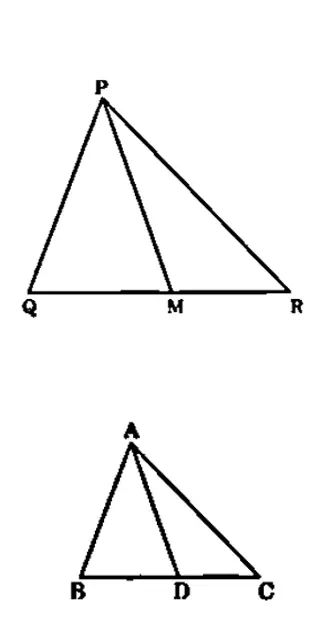
प्रश्न 12: एक त्रिभुज ABC की भुजाएँ AB और BC तथा मध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा मध्यिका PM के समानुपाती हैं (देखिए आकृति)। दर्शाइए कि ΔABC ~ ΔPQR है।
हल:
दिया है : त्रिभुज ABC की भुजाएँ AB और BC तथा मध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा मध्यिका PM के समानुपाती हैं।
सिद्ध करना है: ΔABC ~ ΔPQR
प्रमाण :
AB/PQ = BC/QR = AD/PM ……. (दिया है)
अथवा, AB/PQ = 1/2BC / 1/2QR = AD/PM
अथवा, AB/PQ = BD/QM = AD/PM ——–(1)
(चूंकि मध्यिकाएँ AD और PM BC तथा QR को समद्विभाजित करती हैं।)
अब, ΔABD तथा ΔPQM में,
AB/PQ = BD/QM = AD/PM (समी० (1) से)
ΔABD ~ ΔPQM (S.S.S समरूपता कसौटी से)
∴ ∠B = ∠Q ———(2)
अब, ΔABC तथा ΔPQR में
AB/PQ = BC/QR (दिया है)
और, ∠B = ∠Q (समी० (2) से)
ΔABC ~ ΔPQR (S.A.S समरूपता कसौटी से)
Proved.
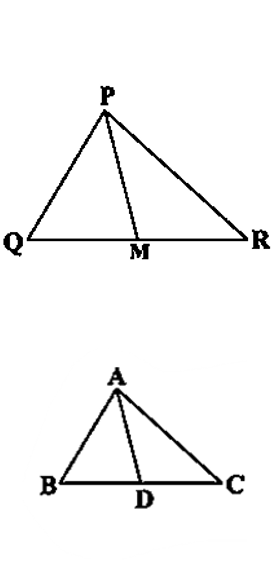
प्रश्न 13: एक त्रिभुज की भुजा पर बिंदु इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA² = CB.CD है।
हल 13:
दिया है : त्रिभुज ABCकी भुजा पर एक बिंदु D इसप्रकार स्थित है की
∠ADC = ∠BAC है
सिद्ध करना है: CA² = CB × CD
ΔADC और ΔBAC में,
∠ADC = ∠BAC [दिया है]
∠ACD = ∠BCA [उभयनिष्ठ]
∴ ΔADC ~ ΔBAC [AA समरूपता कसौटी से]
हम जानते हैं कि समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं। इसलिए
CA/CB = CD/CA
⇒ CA² = CB × CD
Proved
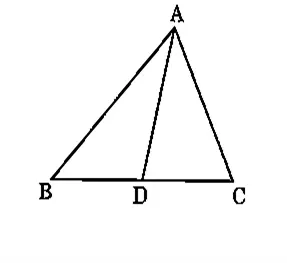
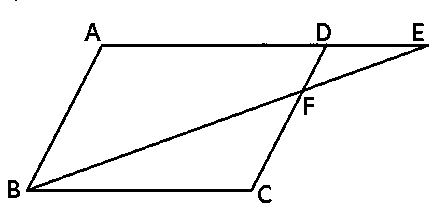
प्रश्न 14: एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज PQR की भुजाएँ PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ΔABC ~ ΔPQR है।
हल 14:
दिया है, AB/PQ = AC/PR = AD/PM AD और PM को क्रमशः बिंदु E और L तक इस प्रकार बढ़ाया ताकि AD = DE तथा PM = DE हो। B को E से, C को E से, Q को L से और R को L से मिलाइए। AD और PM त्रिभुजों की मध्यिकाएँ हैं।
सिद्ध करना है: ΔABC ~ ΔPQR है।
चूँकि AD और PM त्रिभुजों की मध्यिकाएँ हैं। इसलिए BD = DC और QM = MR
तथा, AD = DE [रचना से]
और, PM = ML [रचना से]
चतुर्भुज ABEC भी, विकर्ण AE और BC एक-दूसरे को बिंदु D पर समद्विभाजित करते हैं।
अतः ABEC एक समांतर चतुर्भुज है।
इसी प्रकार, PQLR भी एक समांतर चतुर्भुज है।
∴ AC = BE और AB = EC तथा PR = QL और PQ = LR
दिया है,
AB/PQ = AC/PR = AD/PM
⇒ AB/PQ=BE/QL=2AD/2PM
⇒ AB/PQ=BE/QL=AE/PL
⇒ ΔABE ~ ΔPQL [SSS समरूपता कसौटी से]
हम जानते हैं कि समरूप त्रिभुजों के संगत कोण बराबर होते हैं।
∠BAE = ∠PQL ——(1)
इसी प्रकार ΔAEC ~ ΔPLR और
∠CAE = ∠RPL ——(2)
समीकरण (1) और (2) को जोड़ने पर
∠BAE + ∠CAE = ∠QPL + ∠RPL
⇒ ∠CAB = ∠RPQ —3)
ΔABC और ΔPQR में,
AB/PQ = AC/PR (दिया है)
∠CAB = ∠RPQ [समीकरण (3) से]
∴ ΔABC ~ ΔPQR [SAS समरूपता कसौटी से]
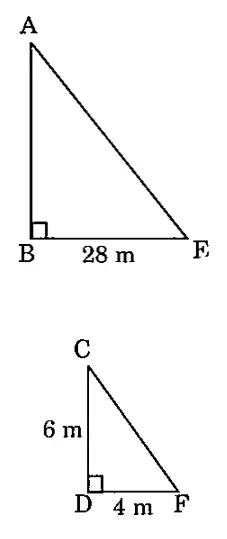
प्रश्न 15: लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
हल 15:
माना CD स्तंभ है और AB मीनार है।
अतः DF स्तंभ की छाया है और BE मीनार की छाया है।
ΔABE और ΔCDF में,
∠DCF = ∠BAE [एक ही समय पर सूर्य का कोण]
∠CDF = ∠ABE [प्रत्येक 90°]
∴ ΔABE ~ ΔCDF [AA समरूपता कसौटी से]
AB/CD = BE/DF
⇒ AB/6 = 28/4
⇒ AB = (28/4) × 6
⇒ AB = 42 m
इसलिए, मीनार की ऊँचाई 42 m है।
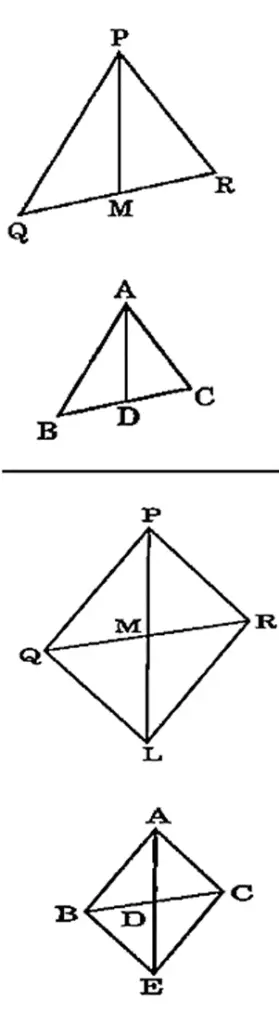
प्रश्न 16: AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ΔABC ~ ΔPQR है। सिद्ध कीजिए कि AB/PQ = AD/PM है।
हल 16:
दिया है : AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएं हैं, जबकि ΔABC ~ ΔPQR है |
सिद्ध करना है : AB/PQ = AD/PM
प्रमाण : ΔABC ~ ΔPQR दिया है |
हम जानते हैं कि समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं।
इसलिए,
AB/PQ = AC/PR = BC/QR ———-(1)
तथा, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ——-(2)
AD और PM त्रिभुज की माध्यिकाएँ हैं।
इसलिए,
BD = BC/2 और QM = QR/2 ——– (3)
समीकरण (1) और (3) से-
AB/PQ = BD/QM —— (4)
ΔABD और ΔPQM में,
∠B = ∠Q [समीकरण (2) से]
AB/PQ = BD/QM [समीकरण (4) से]
∴ ΔABD ~ ΔPQM
AB/PQ = BD/QM = AD/PM [SAS समरूपता कसौटी से]
For students preparing for their Class 10 board exams, the Ultimate Mind-blowing NCERT Class 10 Math 6.3 Solutions offers comprehensive, easy-to-understand answers to all exercise 6.3 problems in the Triangles chapter. This resource simplifies even the toughest questions with clear step-by-step solutions, perfect for Hindi and English medium students alike. Accessible via the permalink ncert-class-10-math-6-3-solutions, it supports effective learning with downloadable PDFs and detailed explanations. Maximize your exam scores and enhance your mathematical skills through these expertly curated solutions that cover every concept necessary to succeed in Class 10 Maths.
Note:
हमारे पास Ultimate Mind-blowing NCERT Class 10 Math 6.3 Solutions की विस्तृत श्रृंखला उपलब्ध है जो कक्षा 10 के छात्रों के लिए बेहद उपयोगी है।
हिंदी माध्यम के छात्रों के लिए हमने एक आसान और समझने योग्य class 10 ncert math solution in hindi तैयार किया है।
चाहे आप बोर्ड की तैयारी कर रहे हों या गृहकार्य, हमारे पास हर विषय के लिए maths class 10 के उत्कृष्ट समाधान हैं।
इस वेबसाइट पर आपको मिलेगा सम्पूर्ण math solution जो खासतौर पर कक्षा 10 के लिए अपडेट किया गया है।
हमें गर्व है कि हम हिंदी में class 10 math solution in hindi प्रदान करते हैं, जिससे छात्र बिना किसी परेशानी के सीख सकें।
Mathematics class 10 के सभी chapters का समग्र हल यहां उपलब्ध है, जिसमें अभ्यास 6.3 के सभी प्रश्न शामिल हैं।
Ultimate Mind-blowing NCERT Class 10 Math 6.3 Solutions के साथ, आप कठिन से कठिन प्रश्न भी आसानी से समझ पाएंगे।
ये class 10 ncert math solution in hindi छात्रों को परीक्षा में बेहतर अंक प्राप्त करने में मदद करेगा।
यहां पर आपको मिलेगा हर टॉपिक का स्पष्ट समाधान, जो आपकी कक्षा 10 की गणित पढ़ाई को आसान करेगा।
हमारे विशेषज्ञों द्वारा तैयार किए गए math solution हिंदी माध्यम छात्रों के लिए एकदम उपयुक्त हैं।
