
Class 10 Math Chapter-6 Ex 6.2 Solutions in Hindi (प्रश्नावली-6.2)
प्रश्न 1:
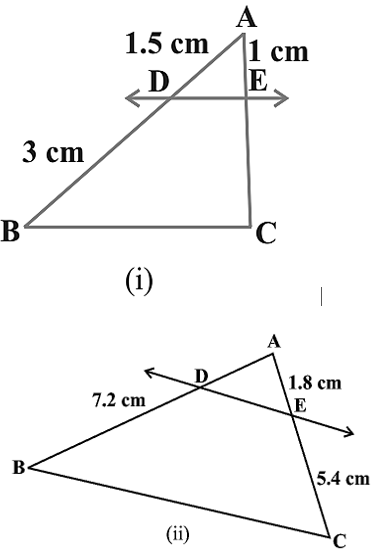
आकृति (i) और (ii) में, DE || BC है। (i) में EC और (ii) में AD ज्ञात कीजिए:
(i)⇒
(ii)⇒
हल 1: (i)
माना EC = x cm
दिया है, DE || BC,
इसलिए,
आधारभूत समानुपातिकता प्रमेय से-
AD / DB = AE / EC
⇒1.5/3 = 1/x
⇒1.5x = 3X1
⇒1.5x = 3
⇒ x=3/1.5=2
इसलिए, EC=2CM {EC=xCM}
प्रश्न 2:
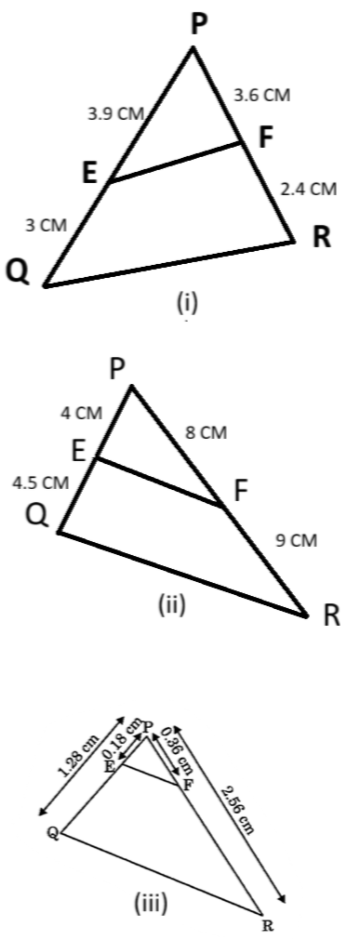
किसी ΔPQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF =0.63 cm
हल 2:
(i) दिया है, PE=3.9cm, EQ=3cm, PF=3.6cm, FR=2.4cm,
इसलिए,
PE/EQ =3.9/3 =1.3
तथा, PF/FR =3.6/2.4 =1.5
क्योंकि, PE/EQ ≠ PF/FR
अतः EF और QR समांतर नहीं हैं।
(ii) दिया है, PE=4cm, QE=4.5cm, PF=8cm, RF=9cm,
इसलिए,
PE/EQ = 4/4.5 =8/9
तथा, PF/FR =8/9
क्योंकि PE/EQ = PF/FR
अतः आधारभूत समानुपातिकता प्रमेय के विलोम से, EF और QR समांतर हैं।
(iii) दिया है, PQ=1.28cm, PR=2.56cm, PE=0.18cm, PF=0.36cm,
इसलिए,
PE/EQ = 0.18/1.28 = 18/128 =9/64
तथा , PF/FR = 0.36/2.56 =9/64
क्योंकि,PE/EQ = PF/FR
अतः आधारभूत समानुपातिकता प्रमेय के विलोम से, EF और QR समांतर हैं।
प्रश्न 3:
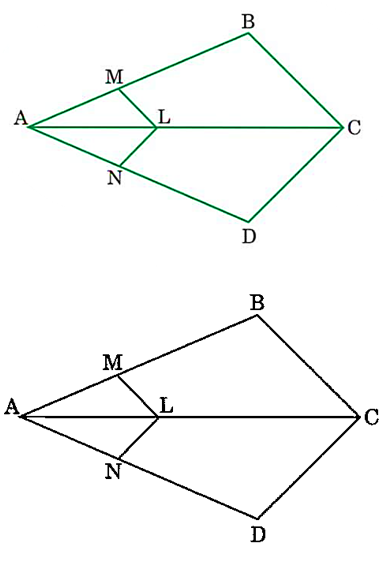
आकृति में, यदि LM || CB और LN || CD हो तो सिद्ध कीजिए कि AM/AB = AN/AD है।
हल 3:
दिया है, △ABC में , LM || CB,
सिद्ध करना है: AM/AB=AN/AD
इसलिए,
आधारभूत समानुपातिकता प्रमेय से-
AM/BM = AL/CL —(1)
इसी प्रकार,
दिया है, △ ADC में, LN || CD,
इसलिए,
आधारभूत समानुपातिकता प्रमेय से-
AN/ND = AL/CL —(2)
समीकरण (1) और (2) से
AM/BM = AN/ND
व्युत्क्रमानुपाती लेने पर-
BM/AM = ND/AN
दोनों तरफ 1 जोरने पर-
1+BM/AM = 1+ND/AN
या, BM+AM/AM = ND+AN/AN
या, AB/AM = AD/AN
पुनः व्युत्क्रमानुपाती लेने पर-
AM/AB = AN/AD
PROVED…
प्रश्न 4:
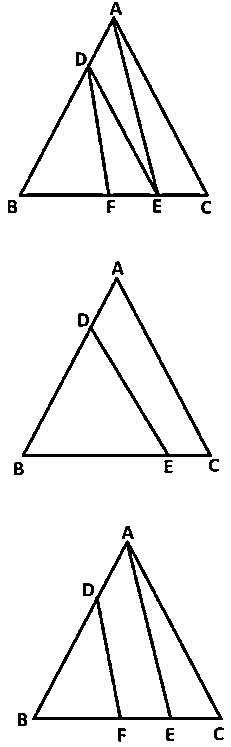
आकृति में, DE || AC और DF || AE है। सिद्ध कीजिए कि BF/FE = BE/EC है।
हल 4:
दिया है, ΔABC में, DE || AC,
सिद्ध करना है: BF/FE = BE/EC
इसलिए,
आधारभूत समानुपातिकता प्रमेय से-
BD/DA = BE/EC — (1)
इसी प्रकार,
ΔABC में, DF || AE,
इसलिए,
आधारभूत समानुपातिकता प्रमेय से-
BD/DA = BF/FE —(2)
समीकरण (1) और (2) से-
BF/FE = BE/EC
PROVED
प्रश्न 5:
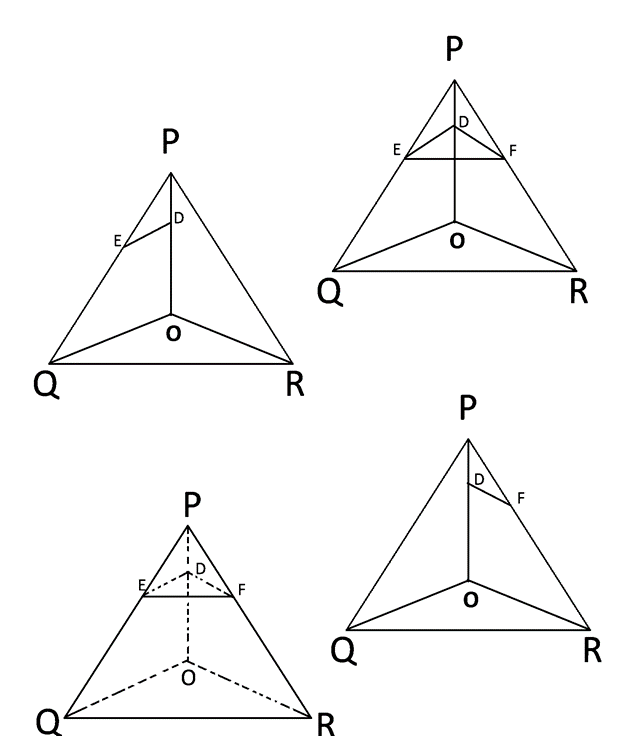
आकृति में, DE // OQ और DF // OR है। दृशाइए कि EF // QR है।
हल 5:
दिया है, ΔPOQ में, DE // OQ,
सिद्ध करना है: EF//QR
इसलिए,
आधारभूत समानुपातिकता प्रमेय से-
PE/EQ = PD/DO ——(1)
इसी प्रकार,
ΔPOR में, DF // OR,
इसलिए,
आधारभूत समानुपातिकता प्रमेय से-
PF/FR = PD/DO —-(2)
समीकरण (1) और (2) से-
PE/EQ = PF/FR
अब, त्रिभुज PQR में,
PE/EQ = PF/FR (ऊपर सिद्ध किया गया है।)
इसलिए,
आधारभूत समानुपातिकता प्रमेय के विपरीत से
EF // QR
PROVED.
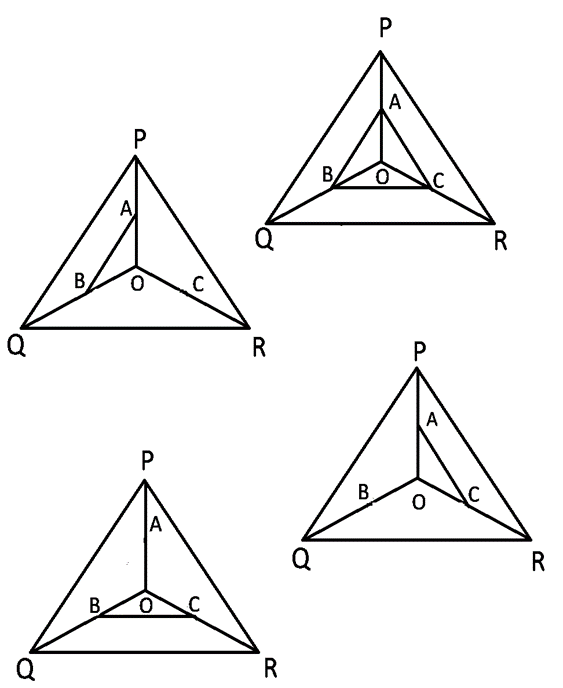
प्रश्न 6: आकृति में, क्रमशः OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि AB // PQ और AC // PR है। दर्शाइए कि BC // QR है।
हल 6:
दिया है, ΔPOQ में, AB // PQ,
सिद्ध करना है: BC//QR
इसलिए,
आधारभूत समानुपातिकता प्रमेय से-
OA/AP = OB/BQ —(1)
इसी प्रकार,
ΔPOR में, AC//PR,
इसलिए,
आधारभूत समानुपातिकता प्रमेय से-
OA/AP = OC/CR —(2)
समीकरण (1) और (2) से,
OB/OQ = OC/CR
अब, त्रिभुज OQR में,
OB/OQ = OC/CR (ऊपर सिद्ध किया गया है)
इसलिए,
आधारभूत समानुपातिकता प्रमेय के विपरीत से-
BC // QR
PROVED.
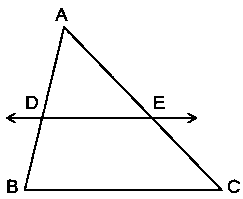
प्रश्न 7: प्रमेय6 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है। (याद कीजिए की आप इसे कक्षा IX में सिद्ध कर चुके हैं)
हल:
दिया है : ABC एक त्रिभुज है जिसकी
भुजा AB का मध्य-बिंदु D है और DE // BC है।
सिद्ध करना है : AE = EC
प्रमाण : ΔABC में-
AD = BD —–(1) दिया है।
DE // BC दिया है।
अतः आधारभूत समानुपातिकता प्रमेय (BPT) से-
AD/BD = AE/CE
या, AD/AD = AE/CE (समीकरण 1 से)
या,1/1 = AE/CE (Bi-cross multiplication)
या, AE = EC
Proved…
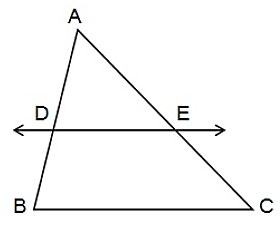
प्रश्न 8: प्रमेय 6.2 का प्रयोग करते हुए सिद्ध कीजिए की एक त्रिभुज की किसी दो भुजाओं के मध्य बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है। (याद कीजिए की आप कक्षा IX में ऐसा कर चुके हैं।)
हल:
दिया है: ABC एक त्रिभुज है जिसकी भुजा AB तथा AC के मध्य-बिंदु क्रमशः D तथा E हैं।
सिद्ध करना है: DE // BC
प्रमाण: ΔABC में,
AD = BD ……….(1) (D, AB का मध्य-बिंदु है)
AE = EC ……….(2) (E, AC का मध्य-बिंदु है)
अब, AD / BD = AE / EC
(क्योंकि दोनों पक्ष 1/1 के बराबर हैं; समीकरण 1 और 2 से)
यानी AD/BD = AE/EC = 1/1
अब,
आधारभूत समानुपातिकता प्रमेय (BPT) के विपरीत से-
(यदि किसी त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होगी।)
इसलिए, DE // BC
PROVED.
प्रश्न 9: ABCD एक समलंब है जिसमें AB // DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिछेद करते हैं | दर्शाइए की AO/BO = CO/DO है |
हल:
दिया है : ABCD एक समलंब है जिसमें AB // CD है | और विकर्ण AC तथा BD एक दूसरे को बिंदु O पर प्रतिछेद करते हैं |
सिद्ध करना है : AO/BO = CO/DO
रचना : बिंदु O से AB // EO खिंचा |
प्रमाण : AB // EO ——–(1) रचना से
AB // CD ——–(2) दिया है |
समीकरण (1) तथा (2) से
EO // CD ——–(3)
△ ABD में
AB // EO (रचना से)
अतः आधारभूत समानुपातिकता प्रमेय (BPT) से-
AE/ED = BO/DO ——-(4)
इसी प्रकार, Δ ADC में,
EO // CD ———(3) से
अतः आधारभूत समानुपातिकता प्रमेय (BPT) से-
AE/ED = AO/CO ——–(5)
समीकरण (4) तथा (5) से-
AO/CO = BO/DO
अथवा, AO/BO = CO/DO [एकान्तरानुपात (Alternando) लगाने पर]
PROVED.
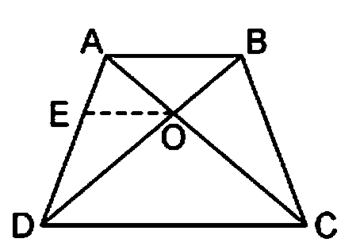
प्रश्न 10: एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिछेद करते हैं कि AO/BO = CO/DO है | दर्शाइए कि ABCD एक समलंब है |
हल:
दिया है: ABCD एक चतुर्भुज है जिसके विकर्ण AC तथा BD एक दूसरे को बिंदु O पर प्रतिछेद करते हैं |
और AO/BO = CO/DO है |
सिद्ध करना है: ABCD एक समलंब है |
रचना: बिंदु O से AB // EO खींचा |
प्रमाण: △ ABD में ,
AB // EO——–रचना से
अतः आधारभूत समानुपातिकता प्रमेय (BPT) से-
∴ AE/ED = BO/DO ——–(1)
जबकि, AO/BO = CO/DO
अथवा, AO/CO = BO/DO ——–(2) [एकान्तरानुपात (Alternando) लगाने पर]
समीकरण (1) तथा (2) से
AE/ED = AO/CO
△ACD की संगत खंड की भुजाएँ समानुपाती हैं | इसलिए आधारभूत समानुपातिक प्रमेय (BPT) के विलोम प्रमेय 6.2 से-
EO // CD ———–(3)
और, EO // AB ————(4) रचना से
समीकरण (3) तथा (4) से
AB // CD
अतः ABCD एक समलंब है |
Proved,

Note :
हमारे पास Class 10 Hindi NCERT Math Solution उपलब्ध हैं जो हिंदी माध्यम के छात्रों के लिए विशेष रूप से तैयार किए गए हैं।
यदि आप class 10 math solution in hindi खोज रहे हैं, तो हमारी वेबसाइट पर आपको हर अध्याय के आसान और सटीक हल मिलेंगे।
इस वेबसाइट पर आपको कक्षा 10 के सभी अध्यायों के लिए Math Solution हिंदी में मिलेगा।
छात्रों के लिए कक्षा 10 गणित सॉल्यूशंस को स्टेप-बाय-स्टेप समझाना हमारा मुख्य उद्देश्य है।
पूरी नींव मजबूत करने के लिए अपने होमवर्क में हमेशा हमारी class 10 math solution का इस्तेमाल करें।
Class 10 Hindi NCERT Math Solution के साथ आप बोर्ड परीक्षा की तैयारी आसानी से कर सकते हैं।
हमारे विशेषज्ञ शिक्षकों द्वारा तैयार किए गए कक्षा 10 गणित सॉल्यूशंस छात्रों को जटिल प्रश्नों को समझने में मदद करते हैं।
कक्षा 10 के छात्रों के लिए हमारी वेबसाइट पर Class 10 Hindi NCERT Math Solution उपलब्ध है, जो हिंदी माध्यम में पढ़ने वाले विद्यार्थियों के लिए विशेष रूप से उपयोगी है।
सभी छात्रों के लिए सरल भाषा में class 10 math solution in hindi प्रदान करना हमारा लक्ष्य है ताकि वे बेहतर समझ सकें।
आप अपनी अपनी पढ़ाई को और मजबूत बनाने के लिए Math Solution हिंदी माध्यम में एक्सरसाइज के साथ यहां पा सकते हैं।
हमें पता है कि कक्षा 10 गणित सॉल्यूशंस का सही और आसान हल होना कितना जरूरी है, इसलिए हमने हर समस्या को विस्तार से समझाया है।
हमारी वेबसाइट से आसानी से डाउनलोड करें class 10 math solution हिंदी में और बोर्ड परीक्षा की तैयारी समय पर शुरू करें।
हमारे द्वारा उपलब्ध कराए गए Class 10 Hindi NCERT Math Solution से आप हर तरह के गणितीय सवालों को आसानी से हल कर पाएंगे।
यातायात की कमी के कारण आप घर बैठकर भी हमारी class 10 math solution in hindi पढ़कर परीक्षा में बेहतर परिणाम ला सकते हैं।
सभी अध्यायों के लिए व्यापक कक्षा 10 गणित सॉल्यूशंस आपको पूरे पाठ्यक्रम को समझने में मदद करते हैं।
Class 10 Hindi NCERT Math Solution आपको जटिल सवालों को आसान बनाने और परीक्षा में आत्मविश्वास बढ़ाने में सहायता करेगा।
हमारे विशेषज्ञ शिक्षकों द्वारा जारी किए गए class 10 math solution डाउनलोड करें और अपनी गणित की तैयारी को और बेहतर बनाएं।
